Análisis estructural con Python I. Una introducción
El análisis estructural es uno de los aspectos elementales para aquellos que nos dedicamos al diseño mecánico o cuestiones similares. En los cursos universitarios de resistencia de materiales se enseñan algunos métodos analíticos que permiten obtener soluciones rápidas para componentes mecánicos simples. No obstante, cuando las geometrías se complican se hace necesario utilizar el enfoque numérico e implementar una metodología de solución utilizando el método de los elementos finitos, el cual proporciona una solución aproximada que será adecuada en medida de ciertos criterios, tales como el tamaño y tipo de elementos, la física del problema, entre otros.
El propósito del presente minicurso es introducir al lector en el uso de las herramientas numéricas que proporciona Python para la solución de problemas de análisis estructural utilizando el método de los elementos finitos.
El método de los elementos finitos consiste en la discretización de un continuo en pequeños elementos, con la finalidad de establecer un sistema de ecuaciones que describa de manera aproximada el comportamiento individual y global del sistema, pasando por la inclusión de las condiciones de frontera y todas las consideraciones físicas que deriven en la simplificación del problema.
En análisis numérico estructural el método de los desplazamientos o de la rigidez, asume que los desplazamientos nodales son las variables desconocidas y comúnmente se debe resolver una ecuación algebraica del tipo:
$$ K U = F $$Donde $F$ es el vector de fuerzas nodales, $K$ la matriz global de rigidez y $U$ el vector de desplazamientos nodales.
Dado que normalmente los desplazamientos son las incógnitas, se tiene que:
$$ U = K^{-1} F $$En el caso de un análisis estático lineal esta ecuación se resuelve como se muestra: calculando la inversa de la matriz rigidez y multiplicando por el vector de fuerzas nodales, para el caso de un análisis no lineal se utilizan métodos iterativos.
La matriz global $K$ se obtiene de ensamblar todas las matrices de rigidez por elemento acorde a la numeración o posición de sus nodos.
Un caso muy simple: elementos resorte¶
El elemento resorte es el elemento finito más simple, tiene un grado de libertad (por cada nodo): traslación en dirección axial.
La matriz de rigidez para un elemento resorte viene dada por:
$$ k^{(e)} = \begin{bmatrix} k_e & - k_e \\ - k_e & k_e \\ \end{bmatrix} $$La obtención de la matriz de rigidez puede consultarla en la mayoría de los libros introductorios de elementos finitos, por ejemplo en [1]. En lo anterior $k_e$ es la rigidez característica del resorte.
Para ejemplificar cómo funciona el método de los elementos finitos en elementos de este tipo vamos a resolver el siguiente ejemplo.
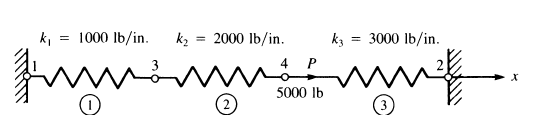
Primero, las matrices de rigidez por elemento vienen dadas por:
$$ k^{(1)} = \begin{bmatrix} 1000 & -1000 \\ -1000 & 1000 \\ \end{bmatrix} \,\,\,\,\,\,\,\, ; k^{(2)} = \begin{bmatrix} 2000 & -2000 \\ -2000 & 2000 \\ \end{bmatrix} \,\,\,\,\,\,\,\, ; k^{(3)} = \begin{bmatrix} 3000 & -3000 \\ -3000 & 3000 \\ \end{bmatrix} $$La matriz global se obtiene ensamblando las matrices elementales utilizando el principio de superposición, es decir, asumiendo que los efectos individuales de cada elemento a la matriz global pueden adicionarse de manera independiente. Para esto se debe expandir la matriz de rigidez elemental y rellenar sólo las posiciones correspondientes a los nodos que componen el elemento.
Por ejemplo, el elemento 1 está conformado por los nodos 1 y 3, entonces:
$$ K^{(1)} = \begin{bmatrix} 1000 & 0 & -1000 & 0\\ 0 & 0 & 0 & 0 \\ -1000 & 0 & 1000 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} $$Mismo caso para los otros elementos:
$$ K^{(2)} = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 2000 & -2000 \\ 0 & 0 & -2000 & 2000 \\ \end{bmatrix} $$$$ K^{(3)} = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 3000 & 0 & -3000 \\ 0 & 0 & 0 & 0 \\ 0 & -3000 & 0 & 3000 \\ \end{bmatrix} $$Luego, la matriz global de rigidez se obtiene sumando las matrices elementales expandidas:
$$ K = \begin{bmatrix} 1000 & 0 & -1000 & 0 \\ 0 & 3000 & 0 & -3000 \\ -1000 & 0 & 3000 & -2000 \\ 0 & -3000 & -2000 & 5000 \\ \end{bmatrix} $$Quedando el sistema de ecuaciones como:
$$\begin{bmatrix} 1000 & 0 & -1000 & 0 \\ 0 & 3000 & 0 & -3000 \\ -1000 & 0 & 3000 & -2000 \\ 0 & -3000 & -2000 & 5000 \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \\ u_3 \\ u_4 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 5000 \end{bmatrix} $$import numpy as np
import numpy.linalg as la
# Datos iniciales
k1 = 1000.0
k2 = 2000.0
k3 = 3000.0
P = 5000.0
# Matrices por elemento
K1 = np.array([[k1,-k1],[-k1,k1]])
K2 = np.array([[k2,-k2],[-k2,k2]])
K3 = np.array([[k3,-k3],[-k3,k3]])
# Matriz global
K = np.array([[ K1[0,0], 0, K1[0,1], 0],
[ 0 , K3[0,0], 0, K3[0,1]],
[ K1[1,0], 0, K1[1,1]+K2[0,0], K2[0,1]],
[ 0, K3[1,0], K2[1,0], K2[1,1]+K3[1,1]]])
F = np.array([0, 0, 0, P])
# Condiciones de frontera
# Nodos 1 y 2 conocidos -> UX = 0
KS = K[2:,2:]
FS = F[2:]
# Resolviendo
USOL = la.solve(KS, FS)
# Vector de desplazamientos
USOL = np.concatenate(([0,0],USOL))
# Obteniendo las fuerzas nodales
NF = np.dot(K,USOL)
# Presentando los resultados
for nodo in range(4):
print("%g UX = %-8.4f FX = %-8.4f"%(nodo+1, USOL[nodo], NF[nodo]))
Utilizando NuSA: una librería para análisis estructural¶
NuSA es una librería Python para el análisis estructural, que facilita el planteamiento y la solución de este tipo de análisis mediante una colección de clases que reciben como dato de entrada las características elementales de un modelo: coordenadas modales, propiedades del material, condiciones de frontera, etc., y retorna valores de salida básicos como desplazamientos y fuerzas.
Para testear las capacidades de NuSA vamos a resolver el ejemplo del elemento resorte. Lo primero es importar las clases que usaremos: Node, Spring y SpringModel.
from nusa.core import Node
from nusa.element import Spring
from nusa.model import SpringModel
Luego creamos un modelo de tipo Spring utilizando la clase SpringModel:
m1 = SpringModel("Modelo 01")
print(m1)
Ahora creamos los nodos que conformarán el elemento resorte:
n1 = Node((0,0))
n2 = Node((0,0))
n3 = Node((0,0))
n4 = Node((0,0))
En este caso no es necesario especificar las coordenadas nodales dado que un elemento resorte sólo necesita la rigidez para la formulación, así que se pueden dejar ambos nodos con coordenadas (0,0).
Enseguida se define un elemento de tipo SpringElement, cuyos datos de entrada son una tupla con los nodos que le conforman y la rigidez del elemento.
e1 = Spring((n1,n3),1000)
e2 = Spring((n3,n4),2000)
e3 = Spring((n4,n2),3000)
Una vez se han definido los nodos y elementos se procede a agregar estos al modelo creado.
m1.add_node(n1)
m1.add_node(n2)
m1.add_node(n3)
m1.add_node(n4)
m1.add_element(e1)
m1.add_element(e2)
m1.add_element(e3)
Luego, establecemos las condiciones de frontera y la carga externa aplicada. Finalmente utilizamos el método solve e imprimimos los resultados obtenidos.
m1.add_constraint(n1, ux=0)
m1.add_constraint(n2, ux=0)
m1.add_force(n4, (5000,))
m1.solve()
for nodo in m1.get_nodes():
print("%s UX = %-8.4f FX = %-8.4f"%(nodo.label,nodo.ux,nodo.fx))
Referencias¶
- [1] Logan, D. L. (1986). A first course in the finite element method. Boston: PWS Engineering.
- [2] Zienkiewicz, O. C., Taylor, R. L., Zhu, J. Z., Zienkiewicz, O. C., & Zienkiewicz, O. C. (2005). The finite element method: Its basis and fundamentals. Oxford: Elsevier Butterworth-Heinemann.
Comentarios
Comments powered by Disqus