Las grillas o conjunto de celdas se utilizan para mostrar conjuntos de datos numéricos y/o cualquier otro tipo en una interfaz sencilla y muy similar a las tradicionales celdas de las hojas de cálculos.
En wxPython para crear una grilla debemos importar el módulo wx.grid y utilizar la clase Grid de dicho módulo. Para inicializar/instanciar un objeto de la clase Grid debemos pasarle como argumentos mínimos el objeto padre y un ID, y enseguida debemos definir el número de filas y columnas que compondrán la grilla utilizando el método CreateGrid, tal cómo se observa en el siguiente ejemplo:
# -*- coding: utf-8 -*-
import wx
import wx.grid as wxgrid
class TestFrame(wx.Frame):
def __init__(self,parent,title):
wx.Frame.__init__(self,parent=parent,title=title,size=(250,250))
self.grid = wxgrid.Grid(self, -1)
self.grid.CreateGrid(10,2)
self.Centre(True)
self.Show()
if __name__=='__main__':
app = wx.App()
fr = TestFrame(None, "Test Grid")
app.MainLoop()
Insertando valores
Y ahora, ¿cómo insertamos valores en cada celda?. Para rellenar las celdas de una grilla utilizamos el método SetCellValue, pasando como argumentos la posición fila-columna de la celda y un string con el valor a insertar. Algo como:
self.grid.SetCellValue(fila,columna,valor)
Donde fila y columna son valores enteros que especifican la posición de la celda y valor una cadena de caracteres. Veamos el siguiente ejemplo:
# -*- coding: utf-8 -*-
import wx
import wx.grid as wxgrid
class TestFrame(wx.Frame):
def __init__(self,parent,title):
wx.Frame.__init__(self,parent=parent,title=title,size=(250,250))
filas = 10
columnas = 2
self.grid = wxgrid.Grid(self, -1)
self.grid.CreateGrid(filas,columnas)
for i in range(filas):
for j in range(columnas):
valor = "(%s,%s)"%(i,j)
self.grid.SetCellValue(i,j,valor)
self.Centre(True)
self.Show()
if __name__=='__main__':
app = wx.App()
fr = TestFrame(None, "Test Grid")
app.MainLoop()
Modificando el color de celdas
Para modificar el color de una celda debemos utilizar el método SetCellBackgroundColour al cual se le pasan como argumentos la posición de la celda y el color a usar (en forma de cadena hexadecimal o bien mediante la clase wx.Colour). En el siguiente ejemplo se muestra como colorear las filas impares de un color determinado:
# -*- coding: utf-8 -*-
import wx
import wx.grid as wxgrid
class TestFrame(wx.Frame):
def __init__(self,parent,title):
wx.Frame.__init__(self,parent=parent,title=title,size=(250,250))
filas = 10
columnas = 2
self.grid = wxgrid.Grid(self, -1)
self.grid.CreateGrid(filas,columnas)
# Asignando valores
for i in range(filas):
for j in range(columnas):
valor = "(%s,%s)"%(i,j)
self.grid.SetCellValue(i,j,valor)
# Modificando el color de fondo
for ii in range(0,filas,2):
for jj in range(columnas):
self.grid.SetCellBackgroundColour(ii,jj,"#fafa77")
self.Centre(True)
self.Show()
if __name__=='__main__':
app = wx.App()
fr = TestFrame(None, "Test Grid")
app.MainLoop()
Para quitar las etiquetas de filas, que a veces pueden resultar poco convenientes, puede utilizar el método SetRowLabelSize y pasar 0 (cero) como argumento.
self.grid.SetRowLabelSize(0)
Personalizando encabezados y anchos de columnas
Los encabezados (headers) de columnas por defecto están rotulados como en una hoja de cálculo (letras en orden alfabético), pero pueden personalizarse utilizando el método SetColLabelValue. Además también puede modificarse el ancho por defecto que tienen las columnas mediante el método SetColSize. En el siguiente ejemplo se muestra lo mencionado anteriormente:
# -*- coding: utf-8 -*-
import wx
import wx.grid as wxgrid
from random import randint
class TestFrame(wx.Frame):
def __init__(self,parent,title):
wx.Frame.__init__(self,parent=parent,title=title,size=(250,250))
filas = 10
columnas = 2
self.grid = wxgrid.Grid(self, -1)
self.grid.CreateGrid(filas,columnas)
self.grid.SetRowLabelSize(0)
# Asignando valores aleatorios
for i in range(filas):
for j in range(columnas):
valor = "%g"%(randint(1,100))
self.grid.SetCellValue(i,j,valor)
# Modificando el color de fondo
for ii in range(0,filas,2):
for jj in range(columnas):
self.grid.SetCellBackgroundColour(ii,jj,"#fafa77")
# Modificando los encabezados y anchos de columna
encabezados = ["Tiempo (s)", "Amplitud (mm)"]
anchos = [100, 100]
for n,col in enumerate(range(columnas)):
self.grid.SetColLabelValue(col,encabezados[n])
self.grid.SetColSize(col,anchos[n])
self.Centre(True)
self.Show()
if __name__=='__main__':
app = wx.App()
fr = TestFrame(None, "Test Grid")
app.MainLoop()
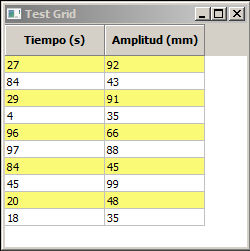
Y bueno, hasta aquí esta entrada introductoria al uso de grillas en wxPython, ya estaremos viendo posteriormente características más avanzadas que permitan personalizar mejor una grilla.
Y una mini-aplicación
A continuación se adjunta una mini-aplicación en la cual se utiliza un grilla de 2x2 para emular los elementos de una matriz de 2x2, de la cual habrá de calcularse el determinante. Esta mini-aplicación incluye algunas consideraciones básicas sobre eventos en la grilla que posiblemente resulten de utilidad para el lector:
# -*- coding: utf-8 -*-
import wx
import wx.grid as wxgrid
class TestFrame(wx.Frame):
def __init__(self,parent,title):
wx.Frame.__init__(self,parent=parent,title=title,size=(200,200))
self.panel = wx.Panel(self, -1)
self.sz = wx.BoxSizer(wx.VERTICAL)
# Grilla
filas = 2
columnas = 2
self.grid = wxgrid.Grid(self.panel, -1)
self.grid.CreateGrid(filas,columnas)
self.grid.SetRowLabelSize(60)
for col in range(columnas):
self.grid.SetColSize(col, 60)
self.grid.SetColLabelValue(col, "%s"%(col+1))
# Campo de texto para resultados
self.res = wx.TextCtrl(self.panel, -1, u"", style=wx.TE_CENTRE)
# Botón para calcular
self.bt = wx.Button(self.panel, -1, u"Calcular")
# Agregando elementos al sizer
self.sz.Add(self.grid, 5, wx.EXPAND|wx.ALL, 2)
self.sz.Add(self.res, 1, wx.EXPAND|wx.ALL, 2)
self.sz.Add(self.bt, 1, wx.ALIGN_CENTRE|wx.ALL, 2)
# Conectando eventos
self.Bind(wx.EVT_BUTTON, self.OnCalc, self.bt)
self.Bind(wxgrid.EVT_GRID_CELL_CHANGED, self.OnCellEdit)
self.panel.SetSizer(self.sz)
self.Centre(True)
self.Show()
def OnCalc(self,event):
"""
Ejecuta el cálculo del determinante, utilizando
como punto de entrada la matriz obtenida mediante
el método GetMatrix. El resultado obtenido se
muestra en el TextCtrl destinado para tal uso.
"""
M = self.GetMatrix()
if M is None:
wx.MessageBox("Rellene todas las celdas...")
return None
det = (M[0][0]*M[1][1]) - (M[0][1]*M[1][0])
res = "det(M) = %s"%(det)
self.res.SetValue(res)
def GetMatrix(self):
"""
Construye una lista de listas para
representar una matriz de 2x2.
"""
rows = self.grid.GetNumberRows()
cols = self.grid.GetNumberCols()
M = []
for row in range(rows):
_crow = []
for col in range(cols):
cval = self.grid.GetCellValue(row,col)
if not cval:
return None
_crow.append(float(cval))
M.append(_crow)
return M
def OnCellEdit(self,event):
"""
Verifica que el valor introducido en una
celda sea un número, de lo contrario elimina el valor.
"""
ii,jj = event.GetRow(), event.GetCol()
inval = self.grid.GetCellValue(ii,jj)
try:
cnum = float(inval)
except:
self.grid.SetCellValue(ii,jj,"")
if __name__=='__main__':
app = wx.App()
fr = TestFrame(None, "Determinante")
app.MainLoop()